Logaritmo: Passo a passo para aprender a calcular Log de jeito fácil
Logaritmo: o que é e o que significa?
Logaritmo: antes de mais nada, o que é e o que significa? Vamos começar com um exemplo para você entender bem.
2 elevado à x = 8
Neste exemplo, temos o X no expoente, sendo essa uma equação exponencial. Qual é o nosso objetivo aqui? Igualar as bases. Neste caso, nós podemos escrever o 8 como uma potência de 2. Sendo assim, temos o seguinte cenário:
2 elevado à x = 2³
E como as bases são iguais, os expoentes são iguais também. Logo, x = 3.
Agora vamos observar um caso diferente: 2 elevado à x = 5
Aqui, não conhecemos um expoente do 2 que dê 5, então precisamos criar uma linguagem matemática que representasse este expoente e é aí que entra o logaritmo. Logaritmo nada mais é do que o expoente do 2. Com isso, podemos escrever:
x = log 5 na base 2
Então, toda vez que você for estudar logaritmo lembre-se que ele é expoente.
Os 3 pré-requisitos para trabalhar com logaritmo
Para você trabalhar certinho com logaritmo e não ter problemas, existem 3 pré-requisitos que você precisa seguir. São eles:
Potenciação
Conheça muito bem a potenciação, as definições e propriedades.
Radiciação
Todas as propriedades, principalmente quando tem o expoente como uma fração.
Exponenciais
A base do logaritmo, que surge principalmente em situações onde não conseguimos a mesma base.
Visto esses 3 temas, podemos começar a definir logaritmos. Vamos lá?
Definições
Temos aqui log de b na base a = c, sendo:
a = base
b = logaritmando
c = logaritmo
Lembre-se do que comentamos acima: logaritmo é expoente. Então, quando nós queremos o log de b na base a, queremos o expoente do a para que dê b. Na imagem abaixo vai ficar mais fácil de visualizar esta representação:
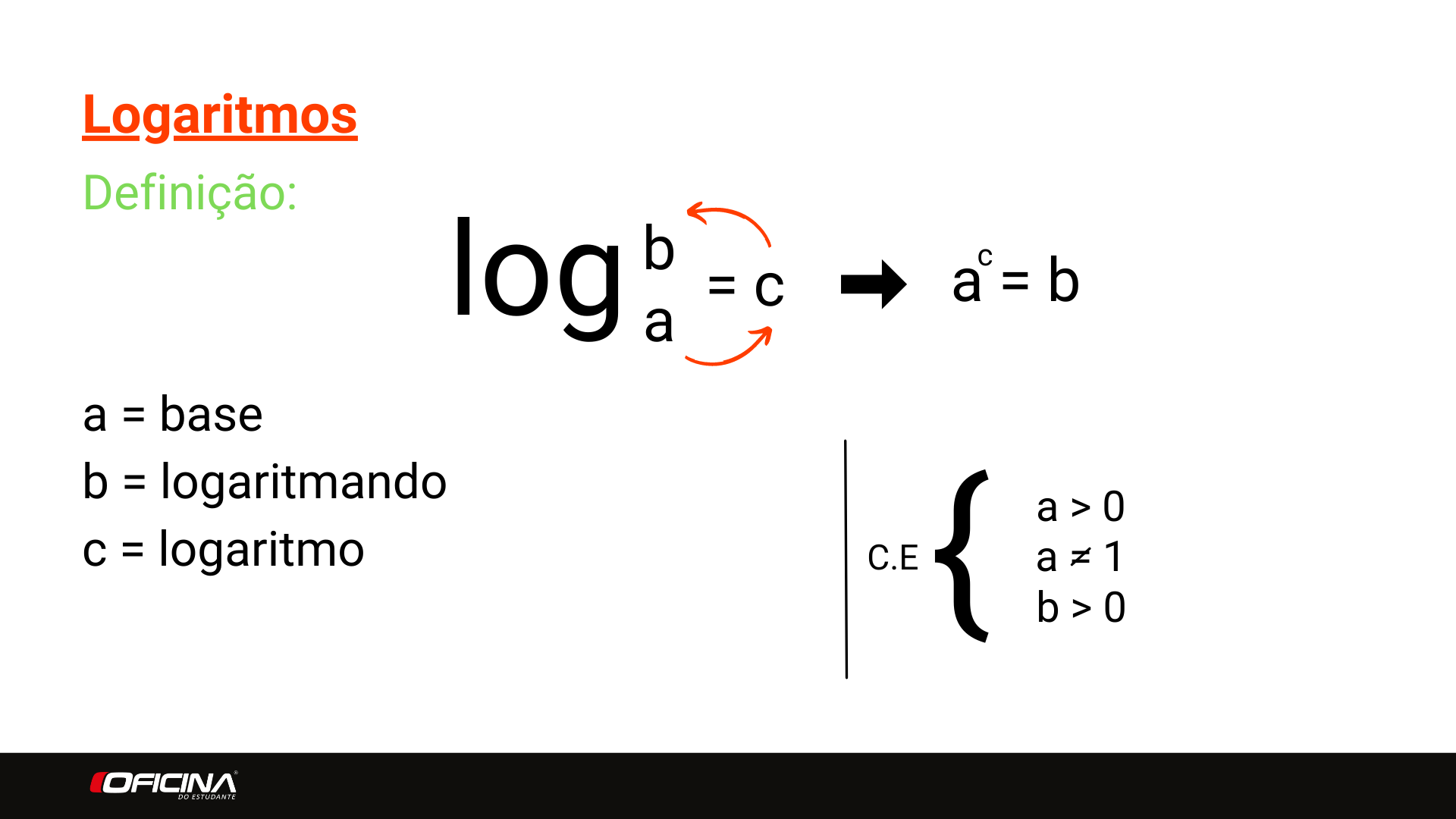
Logaritmo – Definição
Se puder, faça essas flechas, pois elas te ajudarão a lembrar. Desta forma, podemos escrever a elevado a c = b. Essa é uma relação direta com o exponencial. Justamente por isso, nós temos algumas condições de existência:
O a, que é a nossa base, precisa ser sempre positivo, maior que 0 (zero), e diferente de 1 (um).
Já o b, ele é o resultado de uma potência de base positiva, logo ele sempre será um número positivo.
Tendo isso, o c – que é o nosso logaritmo, será qualquer número real.
Exemplo prático de logaritmo
log de 32 na base 2 = c
Pensou em logaritmo, pensou em expoente. Então, qual é o expoente do 2, para que esse resultado dê 32? Com isso, temos uma equação exponencial:
2 elevado à c = 32
2 elevado à c = 2 elevado à 5 (já que 32 pode ser escrito como uma potência de base 2). Assim, temos bases iguais, então os expoentes também são iguais. Logo:
c = 5
Então, o logaritmo de 32 na base 2, é 5.
Consequências da definição
Nós temos 4 relações que são chamadas de consequências da definição. O que isso significa na prática? Elas são resultados de logaritmo que você pode concluir direto, sem precisar passar por todo o processo que vimos anteriormente. Vamos avaliar um por um:
log de a na base a:
No primeiro caso, o logaritmando e a base são iguais. Neste caso, se o logaritmo é expoente, nós queremos o expoente de a para que esse resultado dê a. Com isso, temos que pensar “a elevado à quanto dá a?”, e a resposta é bem simples, já que sabemos que todo número elevado à 1, é ele mesmo.
Importante lembrar: qualquer dos casos onde isso possa não acontecer, com uma base 1 (um) ou uma base o (zero), já são excluídos lá na condição de existência.
log de 1 na base a:
a elevado à alguma coisa tem que dar 1 (um). Também é bem simples, já que sabemos que todo número elevado à o (zero), é 1 (um). Então o log de 1, vai dar sempre 0 (zero).
log de a elevado à n na base a:
O que queremos aqui é o a elevado à ‘alguém’ que dê como resultado a elevado à n (sendo esse n como qualquer número real). Então, a elevado à n, só pode ser igual à a elevado à n, não é mesmo? Lembre-se: toda vez que o logaritmando for uma potência com a base igual à base do logaritmo, o resultado é o próprio expoente.
a elevado à log de b na base a:
Para fechar as consequências, nós temos a elevado à log de b na base a. Observe que temos uma potência, onde a base desta potência é igual à base do logaritmo. Para que aconteça esta consequência, é fundamental que isso apareça. Então nós queremos a elevado à log de b na base a, mas uma vez que sabemos que log de b na base a é c (explicamos isso na parte de definição de logaritmo), temos o seguinte cenário:
a elevado à c, que é igual à b.
Então toda vez que tivermos uma potência, cujo o expoente for um logaritmo, observe a base do logaritmo. Se ela for igual à base da potência, o resultado é sempre o próprio logaritmando. Veja a imagem abaixo para ficar mais claro:
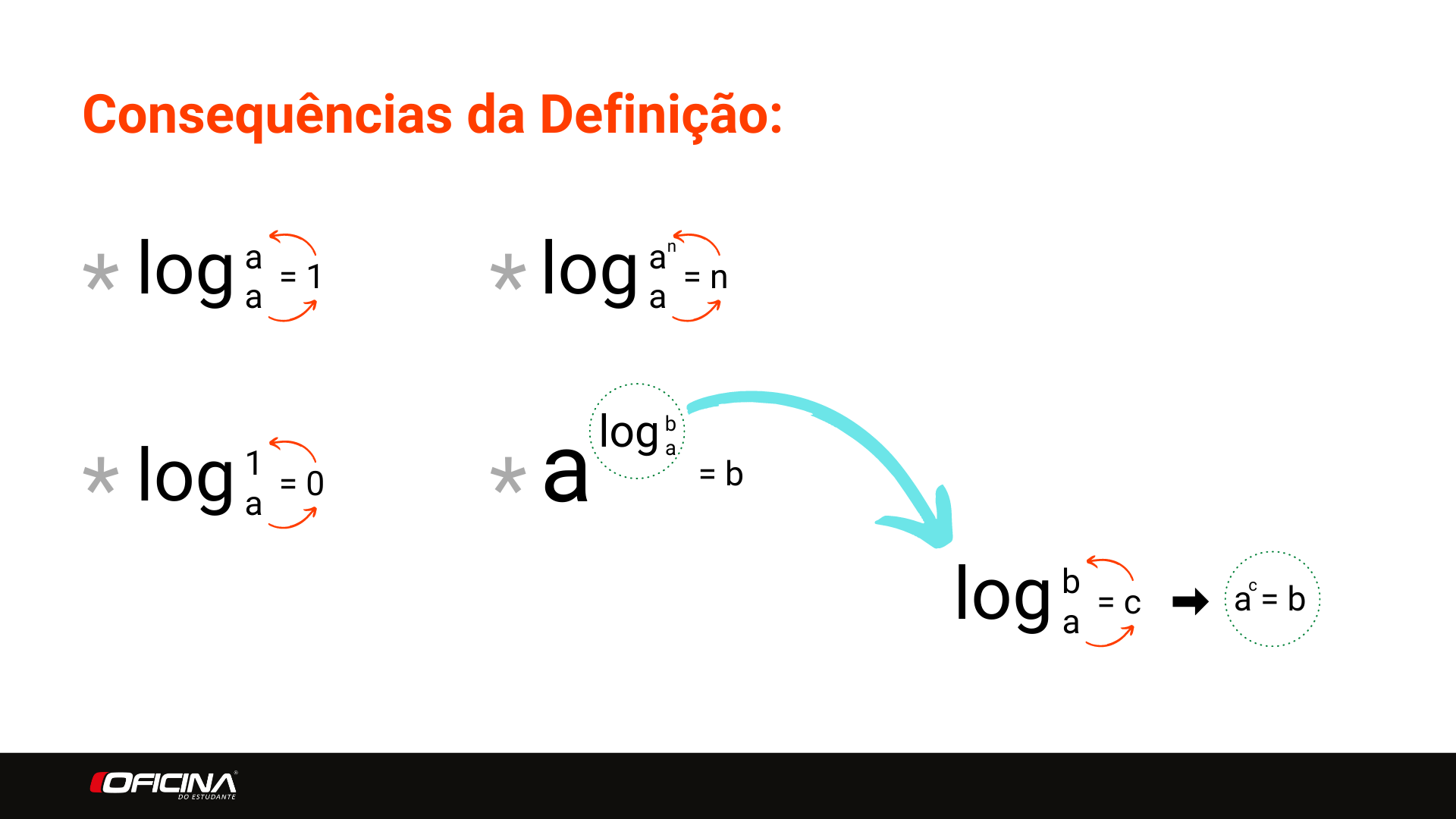
Logaritmo – Consequências da Definição
Se preferir, também temos este conteúdo em formato de vídeo. Se liga na explicação incrível do nosso professor Eduardo:




Deixe uma resposta